GAMES103课程主页:GAMES103:基于物理的计算机动画入门 - 计算机图形学与混合现实研讨会
上一篇:GAMES103笔记 Lecture 7、8 有限元方法(Finite Element Method)
笔者第一次学习计算机图形学的物理部分,笔记中可能存在错误和解释不清的地方,欢迎大佬以及和我一样的萌新来多多交流讨论,对于错误的部分希望能毫不留情的指正。
碰撞检测
碰撞检测的流程(Collision Detection Pipeline)
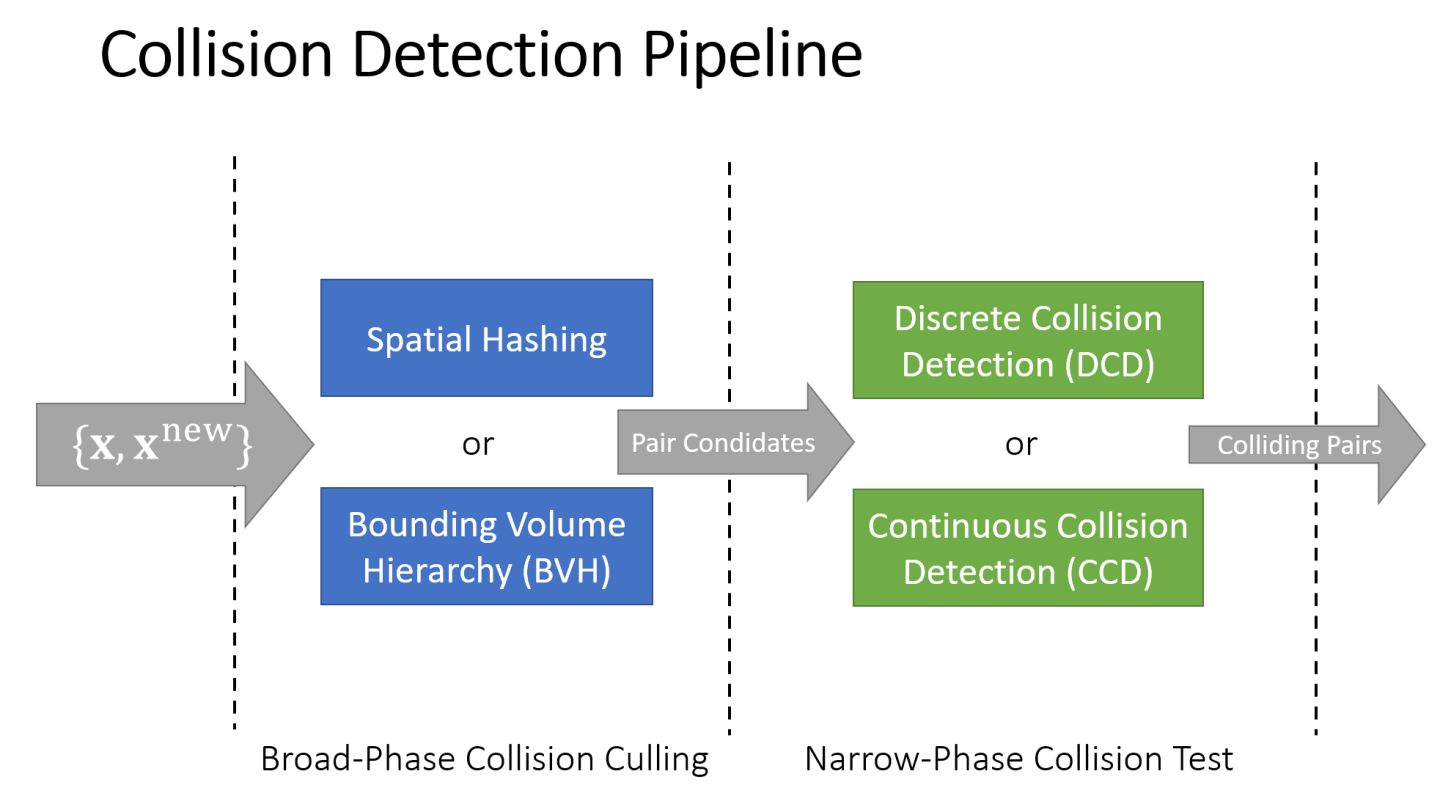
当场景中存在很多物体时,如果直接在所有对象间两两检测是否发生碰撞,时间复杂度是 。
一般的处理流程将碰撞检测分两个阶段。第一阶段(Broad-Phase Collision Culling)先用空间划分的数据结构或BVH快速地排除掉一些不可能发生碰撞的物体对。
第二阶段(Narrow-Phase Collision Test)再对可能发生碰撞的物体做具体的碰撞检测,又分为离散碰撞检测(Discrete Collision Detection, DCD)和连续碰撞检测(Continuous Collision Detection, CCD)。
Spatial Hashing (SH)

空间哈希法,Spatial Hashing (SH),又称空间划分法(Spatial Partitioning),像哈希表一样将空间划分成一个个 bucket,一个 bucket 就是空间中的一个小区域。
不同于一般哈希表,这里一个bucket和物体可以形成多对多的关系。
查询一个物体 A 和其他物体是否发生碰撞时,只需要看与 A 相交的 bucket 还与哪些物体相交,这些物体就是候选的可能发生碰撞的物体,而没有与 A 占据同一空间的物体就可以直接排除掉。
如果物体发生了运动,则需要看它的运动轨迹,运动过程途经的所有 bucket 都要查询。
优化:
三维中需要把空间划分成非常多的小格子,直接存格子占用大量内存。
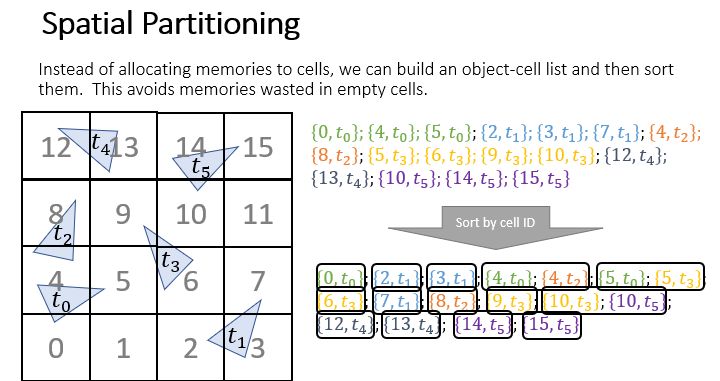
解决方法是只存储物体占有的格子,并且按照格子的序号排序,这样也能快速的通过格子序号来查询格子中的物体。
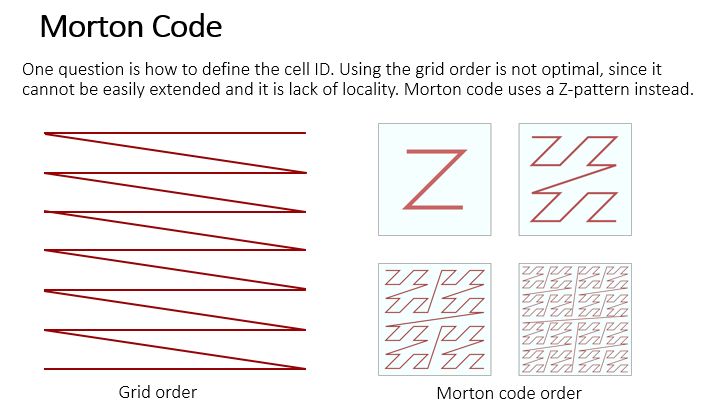
还有一个优化方向是提高访问内存的连续性,按照类似 Z 字型的顺序给格子编号,按照这个顺序去访问格子,提高 Cache 的命中率。
扩展阅读:
Chapter 32. Broad-Phase Collision Detection with CUDA | NVIDIA Developer
BVH (Bounding Volume Hierarchy)

对物体进行划分,用包围盒包住物体,如果包围盒不相交,则包围盒内的物体也不相交。
包围盒形成树状结构(Hierarchy),小包围盒作为子节点,合并后形成大包围盒,对应父节点。
形成树状结构后可以套用很多树的递归算法。
包围盒的类型:
轴对齐包围盒,Axis-aligned bounding box (AABB) ,边界与坐标轴平行,容易计算
球,要用平方距离公式,将距离和球的半径做比较
oriented bounding box (OBB),与物体方向一致的包围盒,提高包围盒的精度,但计算复杂,实际不常用
优化:
相距很近的物体需要搜索到树的底层。在模拟中,形变的地方容易发生相交,Zheng and James. 2012. Energy-based Self-Collision Culling for Arbitrary Mesh Deformations. TOG (SIGGRAPH) 通过定义形变的能量来判断相交的可能性,该方法对于刚体比较有效,对于衣服这种本来就容易出现较大形变的物体效果不好。
SH和SVH的比较

SH 方法容易实现,对 GPU 友好,但是每次更新物体位置都需要重新计算与格子的对应关系。
SVH 的树形结构本身不需要更新,只有包围盒需要更新,实现起来不难,但是其树形结构对 GPU 不友好,且树形结构实现起来可能会遇到一些麻烦。
离散碰撞检测(DCD)
离散碰撞检测(Discrete Collision Detection, DCD)只查询某一时刻两个物体是否发生相交,其直接输入为一个三角形和一条边,更复杂的输入都可以由三角形-边组合而来。
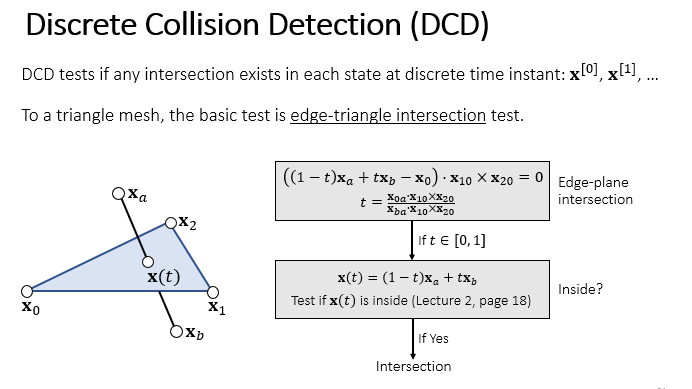
求边和三角形是否相交的思路为先求出边所在直线和三角形所在平面的交点,再看这个交点是否在边上和是否在三角形內。
对于以 和 为端点的边,其所在直线上一点可以表示为 ,且 和 之间的点必定满足 。代入混合积求四面体体积等于0的公式即可求出交点,并且可以直接用 t 的值判断交点是否在边上。之前介绍过用叉乘判断点是否在三角形内部的方法,这里不再重复。
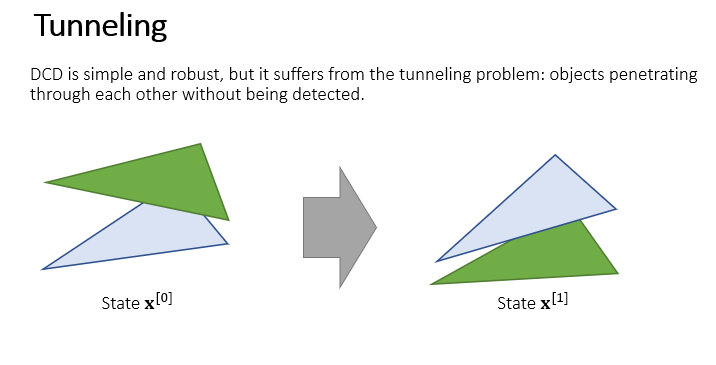
显然,离散碰撞检测存在遂穿(Tunneling)的问题,特别是当物体运动速度非常快且物体比较薄的时候,更容易发生遂穿。
连续碰撞检测(CCD)
连续碰撞检测(Continuous Collision Detection, CCD)的基本输入是点-三角形,边-边。更复杂的输入由这两种情况组合而来。
为什么要做边-边,考虑两个三角形的边以非平行的姿态碰撞,两个三角形嵌套到一起的情况,这时候不存在任意顶点和另一个三角形发生碰撞的情况。
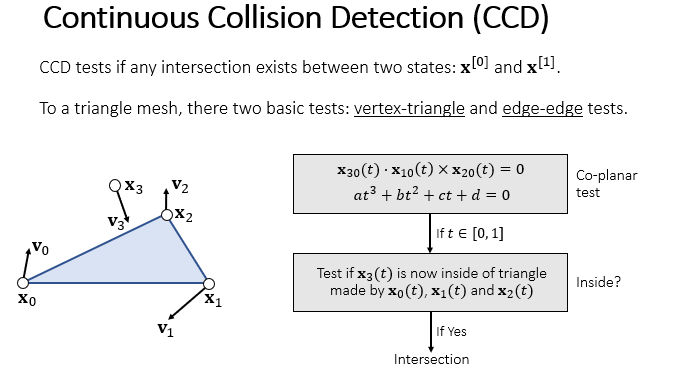
对于点-三角形,一共有4个点,假设每个点在要检测的时间步内速度恒定,则四个点的轨迹都是关于时间 t 的一次函数。把单独的那个点的轨迹看出直线线段,此时问题又转化成了线段和三角形是否存在交点。
依旧用四面体体积公式为 0 的条件,不同之处只在于三角形的三个顶点也在运动。代入混合积得到一个关于 t 的三次方程,如果解出来的时间 t 合法,且交点在三角形内,说明发生碰撞。
注意解三次方程可以用二分法,只需要看[0,1]间是否存在根。如果用求根公式,其中的开根号操作会造成较大的误差。相比于DCD,增加的开销也在于解方程的过程。
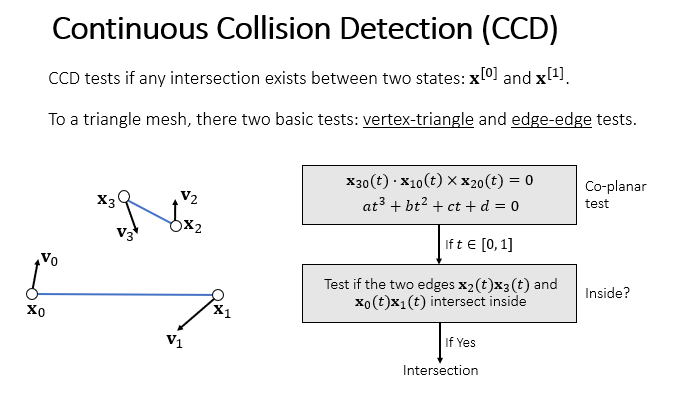
对于边-边,要求出两个边共面的时刻,依然用混合积公式得到三次方程。
如果共面的时刻合法,且两个线段在这个面上有交点,说明发生碰撞。
CCD的缺点:开销大,实现难
扩展阅读
Bridson et al. 2002. Robust Treatment of Collisions, Contact and Friction for Cloth Animation. TOG (SIGGRAPH).
碰撞处理
相交解除(Intersection Elimination)
对于离散碰撞检测,常常不考虑碰撞发生的原因,只需要在碰撞发生后把相交解除掉。允许物体在非常短的时间内存在相交。

对于存在体积的物体,只需要沿着 SDF 的方向把物体推出去。

但是对于非封闭的曲面,如布料,处理起来比较麻烦。
Baraff et al. 2003. Untangling Cloth. TOG (SIGGRAPH) 给了一个解决方案,先对布料分段,认为比较小的那一段发生了相交,如上图的中间部分,解除这一部分即可。
这个方法不好处理边界,并且依赖于对面积的评估,不好在 GPU 上实现。

Volino and Magnenat-Thalmann et al. 2006. Resolving Surface Collisions through Intersection Contour Minimization. TOG (SIGGRAPH). 这篇论文的思路是缩短相交曲线,也存在一些局限性。
内点法和碰撞区域优化方法

连续碰撞检测中,检测到碰撞发生后,想要让物体回到合法的位置,有两种处理的思路。
上图中蓝色区域为合法区域,白色区域为发生碰撞的区域。
内点法(Interior Point Methods)细化模拟的步长,提高模拟的真实性,尽量保证每一步都落在合法范围内。内点法保证永远能模拟到还算合理的结果(相对于发生碰撞的物体相交在一起的结果),但可能要在小步长下走很多步才能达到边界位置。由于物体上所有点的模拟需要同步进行,不仅发生碰撞的点需要走这么多步,其他物体上所有的点都需要跟着走很多步,所以内点法速度比较慢。
碰撞区域优化方法(Impact Zone Optimization)从发生碰撞的位置出发回到合法位置,它只需要处理发生碰撞的那些顶点,且模拟的步长可以设得比较大,运行速度较快。但是可能存在回不到合法区域的情况,尤其是当模拟步长较大,导致碰撞位置离安全区域较远的时候。
Log-Barrier 内点法


Log-Barrier 内点法借助 log-barrier 斥力公式来求解最终的合法位置。
最终位置符合两个条件:离碰撞发生位置越近越好,且不能越过边界。
所以求解最终位置可以看做一个带约束的优化问题。
之前在刚体的碰撞处理中已经提过 log-barrier 公式,物体距离边界越近,斥力越大,正好作为惩罚项代替不能越过边界的约束条件。
最终要优化的目标为
用梯度下降法求解这个问题时要注意步长,如果步长大了可能导致物体跑到边界外。且每优化一步都要检测是否发生了碰撞。
扩展阅读
Bridson et al. 2002. Robust Treatment of Collisions, Contact and Friction for Cloth Animation. TOG (SIGGRAPH).

Impact Zone Optimization 失败以后可以选择内点法或者 Rigid Impact Zones。
Rigid Impact Zones 方法是指检测到碰撞处理时,不进行任何处理,直接退回上一帧并保持不动,Artifact 较大。





