GAMES103笔记 Lecture 6 基于约束的布料模拟方法（Constrained Approaches）

投影操作

真实世界中的布料拉伸超过一定程度后，对拉伸具有很强的抵抗。

基于胡克定律的弹簧模型中需要增大弹性系数k来模拟这种现象，但这会造成显示积分和隐式积分都出现问题，增大了模拟的计算量。

基于约束的方法被提出时的动机就是想要解决这个问题。

先考虑只有一个弹簧的情况，假设弹簧的弹性系数无限大，那么弹簧的长度就成了一个约束，即弹簧的形变量 $\phi(\mathbf{x})=0$ ，右图中 $\Omega$ 是满足这个约束的空间。

当约束被破坏时， $\mathbf{x}=\{\mathbf{x}_i,\mathbf{x}_j\}$ 在 $\Omega$ 外，我们做一个投影操作把 $\mathbf{x}$ 以最近的距离移动到 $\Omega$ 的边界上使弹簧恢复原长。

得到更新公式。

其中 $m_i$ 是端点的质量，默认情况下两端质量相同，拉伸后两个端点都向着中心点移动，如果希望让其中一个端点被固定住不动，只需要把那个端点的质量设为无限大。

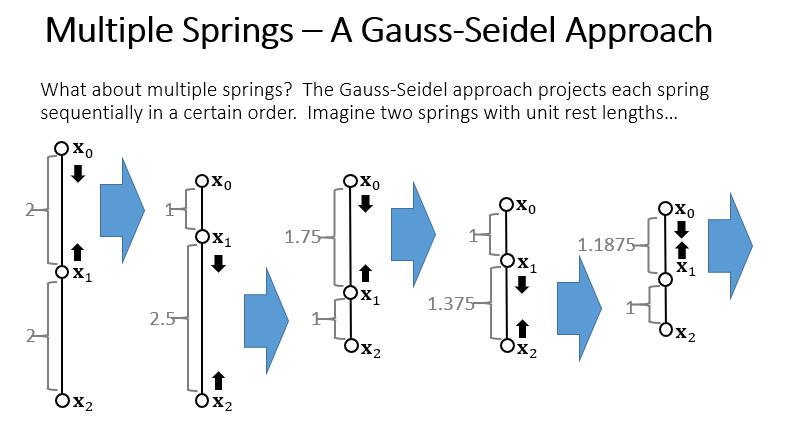
存在多个弹簧时，Gauss-Seidel 方法反复循环处理多个弹簧。

上图两个弹簧的原长都是1，在某一时刻两个弹簧的长度都被拉伸为2。先用刚才的投影操作处理上面的弹簧，上面的弹簧恢复长度1，下面的弹簧长度被拉伸到2.5。再处理下面的弹簧，下面弹簧恢复原长，上面的弹簧又被拉长，再处理上面的弹簧……这样迭代下去两个弹簧的长度都收敛到1。（我觉得这里的迭代操作类似于多个骨骼的 IK 操作）

迭代次数越多，就能更好地满足所有弹簧的约束。

Gauss-Seidel 方法虽然名字叫 Gauss-Seidel，但与数学中的 Gauss-Seidel 其实不一样，实际所做的操作更接近于随机梯度下降算法。

Gauss-Seidel 方法中处理边的顺序很重要，可能会造成 bias 问题（整个布料歪向一边），也可能影响算法收敛的速度。

Jacobi 方法先遍历所有弹簧，把每个点受到多个弹簧影响的位置更新量累加起来取平均值，再用平均值更新弹簧的位置。

Jacobi 方法没有偏向性，不存在 bias 问题。容易并行计算。

收敛速度略慢于 Gauss-Seidel 方法。

PBD (Position Based Dynamics)

PBD方法的整体流程与 Shape Matching 类似。如右图所示，先假装不存在弹簧，自由地更新每个顶点的位置，然后用投影的方法让顶点满足弹簧的约束，更新顶点位置的同时也给顶点加上速度。

PBD方法中不存在物理中弹性系数的概念，布料表现出的弹性与迭代次数和 Mesh 的分辨率有关。

迭代次数多，布料的弹性就小（弹力大，不能被拉伸），迭代次数少，布料的弹性就大（弹力小，可以被拉伸）。

Mesh 的分辨率小，只需要少量迭代位置就收敛了。所以 Mesh 分辨率小布料的弹性就小，Mesh 分辨率大布料的弹性也大。

PBD 方法的优点：容易实现，容易并行，对内存的访问少（只需要更新顶点），被广泛用在游戏引擎和仿真软件中，Nvidia 的 PhysX 物理引擎也采用了 PBD 方法。在低分辨率模型上运行速度快，对不到 1000 个点的网格可以做到实时模拟。

PBD方法的缺点：不符合物理规律，弹性与网格的分辨率和迭代次数有关。无法得到精确解，迭代次数多反而会产生 Locking 问题让布料无法被拉伸。在高分辨率网格上运算效率明显下降。

分层的方法（类似HLOD）可以让 PBD 方法应用在高分辨率网格上，但是会造成一些其他问题。Chebyshev 等加速方法也可以用。

Strain Limiting

Strain 是“应变”，指物体局部的相对变形。

应变在力学中定义为一微小材料元素承受应力时所产生的变形强度(或简称为单位长度变形量)

Strain Limiting 方法可以被认为是对 PBD 的一个改进。

与 PBD 方法的区别在于做投影前 Strain Limiting 方法不只是模拟一个简单的粒子系统，这个步骤中也可以加入弹簧等模型，最后的投影只是一个纠错步骤，保证模拟的稳定性。

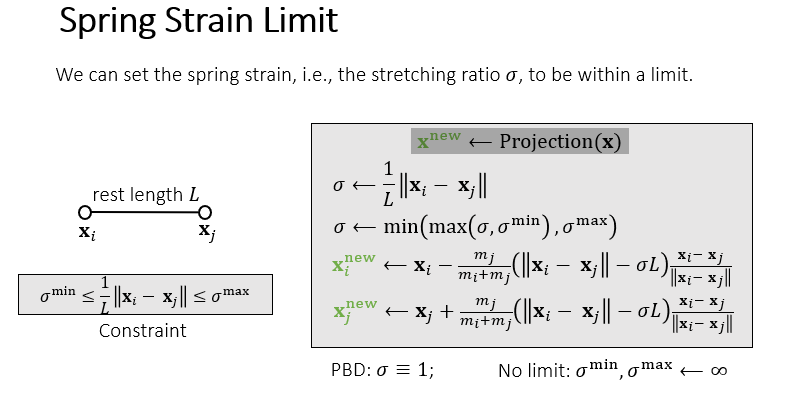
相对的，可以放宽约束条件，投影时不需要让弹簧回到原长，只要回到与原长接近的一定范围内即可。

公式中的 $\sigma$ 代表弹簧的形变量。

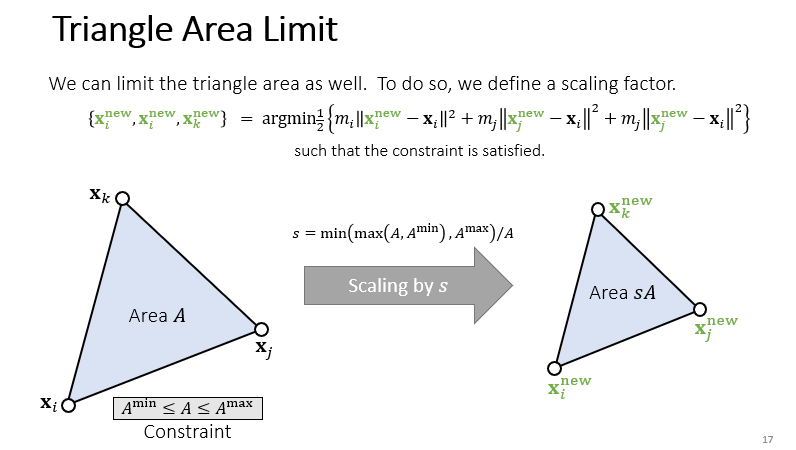
Strain Limiting 方法也可以应用到二维和三维图形上。

这是一个约束三角形面积的例子，当三角的面积超出了约束范围时，直接对三角形进行缩放使面积满足约束。

s 是缩放比。 $\mathbf{c}$ 是质心位置，缩放时质心的位置不变。

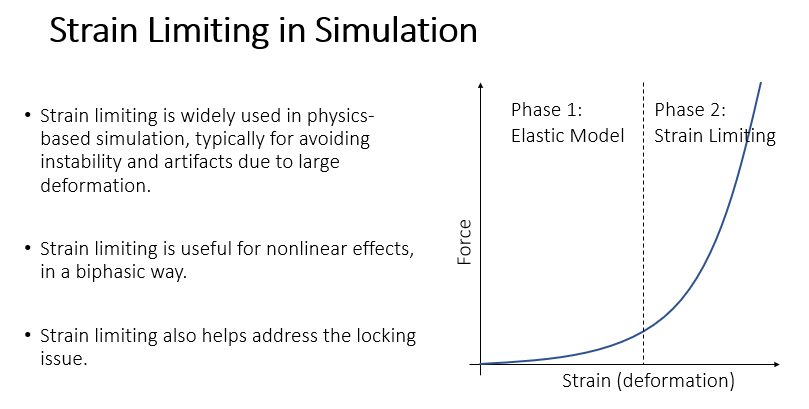
Strain Limiting 方法被广泛用于基于物理的模拟中。很多物体的力与形变量之间存在非线性关系，发生大形变时的表现和小形变时表现出不同的行为，只用一种模型模拟往往会存在数值不稳定的问题，Strain Limiting 方法等同于将形变量分为两段分别进行处理。

Strain Limiting 方法有助于解决 locking issue。因为使用 Strain Limiting 方法后可以在形变量小时使用较小的弹性系数 k，而 locking issue 在 k 较大时比较严重。

PD (Projective Dynamics)

PD 方法和 PBD 一样从约束出发，但根据投影满足约束的操作定义出了能量，之后依然用隐式积分的方法来做模拟。

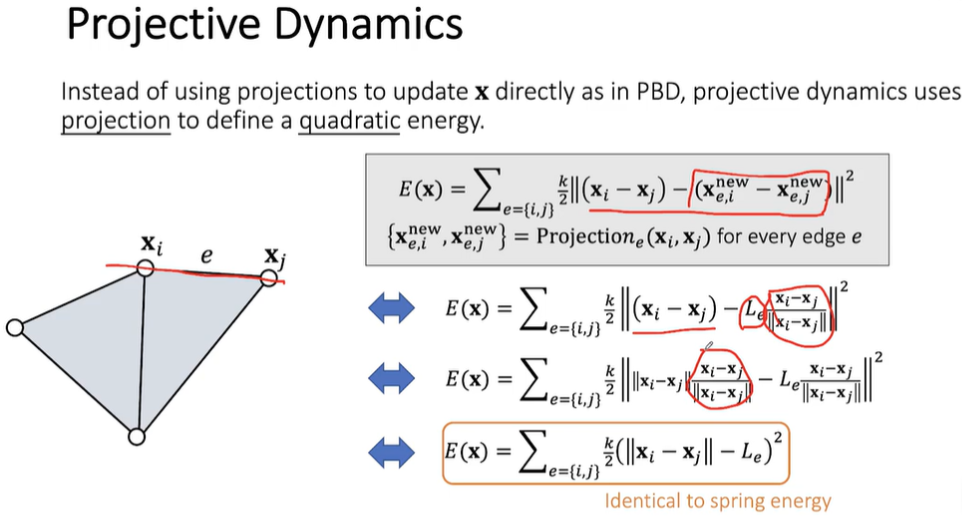
PD 定义的能量其实和之前弹簧模型的能量一模一样，只是换用投影后的新位置来表示。

上图等价公式推导第一步中， $\mathbf{x}_{e,i}^{new} - \mathbf{x}_{e,j}^{new}$ 一定在弹簧原来的方向上且长度等于弹簧原长，所以替换成 $L_e\frac{\mathbf{x}_i-\mathbf{x}_j}{\|\mathbf{x}_i-\mathbf{x}_j\|}$ 。

第三步把 $\frac{\mathbf{x}_i-\mathbf{x}_j}{\|\mathbf{x}_i-\mathbf{x}_j\|}$ 提到求长度的括号外面，又因为其长度为1所以直接去掉。

$E(\mathbf{x})$ 对 $\mathbf{x_i}$ 求梯度得到顶点 i 处的弹力。

假设 $\mathbf{x}_{e,i}^{new}$ 和 $\mathbf{x}_{e,j}^{new}$ 与 $\mathbf{x}_i$ 无关，求得弹力也与弹簧的弹力一致。

求 Hessian 时 PD 方法才出现和原始的物理模拟方法的区别。

依然假设 $\mathbf{x}_{e,i}^{new}$ 和 $\mathbf{x}_{e,j}^{new}$ 与 $\mathbf{x}_i$ 无关，求得的 Hessian 具有非常简单的形式，且为常数矩阵。

这是 PD 方法最大的好处。

模拟的总体步骤和隐式积分一样，区别只在于前面多了一步计算投影的位置，以及使用的 Hessian 矩阵不一样。

由于迭代时 $\Delta x$ 左边是个常数矩阵，用 LU 分解这样的直接法来解线性系统时就只用分解一次，减少了大部分开销。

PD 法也相当于用了一个常数矩阵近似替代隐式积分的 Hessian 简化计算。

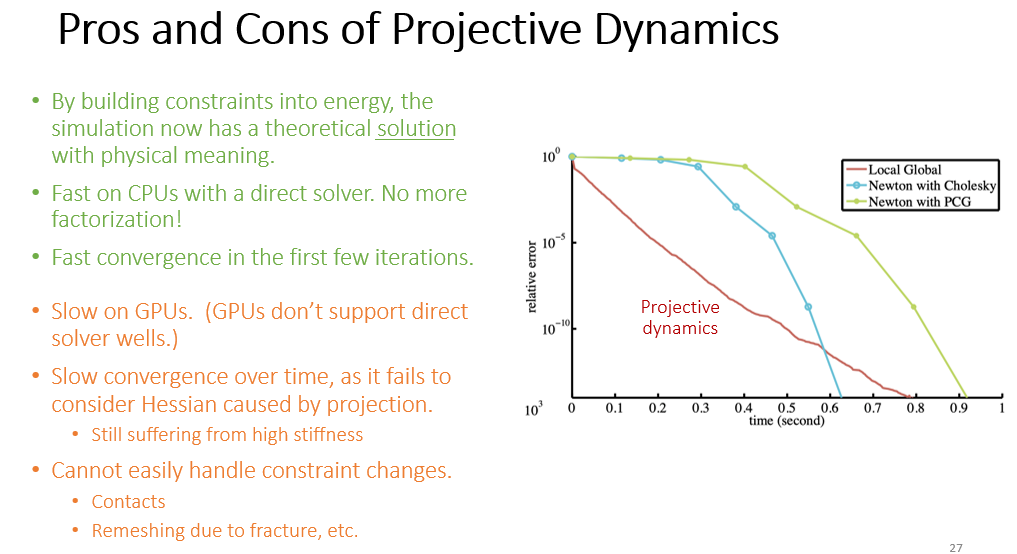
PD 的优点：

• 相对于 PBD，有物理量的定义
• 只需要一次 LU 分解，在 CPU 上效率高
• 如图所示，相对于隐式积分法，PD 前期的计算效率高

PD 的缺点：

• 在 GPU 上慢，因为 GPU 不支持直接法求解线性系统
• 后期的收敛速度不如牛顿法
• 不好处理约束改变的情况

Constrained Dynamics

Constrained Dynamics 方法提出的动机：PBD 方法要做到严格约束弹簧顶点的位置需要很多次迭代。

Constrained Dynamics 可用于用铰链连接的刚体模拟，例如人体骨骼，模拟人体的时候不希望关节之间被拉伸。

Constrained Dynamics 方法的能量公式和隐式积分法相同。

Constrained Dynamics 方法的能量公式和隐式积分法相同。

把约束 $\mathbf{\Phi}(\mathbf{x})$ 代进 $E(\mathbf{x})$ 改写成二次型的形式得到 $E(\mathbf{x})=\frac{1}{2}\mathbf{\Phi}^T(\mathbf{x})\mathbf{C}^{-1}\mathbf{\Phi}(\mathbf{x})$

其中 $\mathbf{C}=diag(\frac{1}{k},\frac{1}{k},...,\frac{1}{k})$ ，称为柔度矩阵（Compliant matrix），因为 $\frac{1}{k}$ 是弹簧劲度系数的倒数所以反应柔度。

$E(\mathbf{x})$ 求梯度得到力的新形式 $\mathbf{f}(\mathbf{x})=\mathbf{J}^T\lambda$

其中 $\mathbf{J}=\frac{\partial\mathbf{\Phi}}{\partial\mathbf{x}}$ 是约束的 Jacobian 矩阵， $\mathbf{\lambda} = - \mathbf{C}^{-1} \mathbf{\Phi}$

把隐式积分更新公式写成动量形式有 $\mathbf{M}\mathbf{v}^{new}-\Delta t\mathbf{J}^T\mathbf{\lambda}^{new}=\mathbf{M}\mathbf{v}$

同时 $\mathbf{C}\mathbf{\lambda}^{new}= -\mathbf{\Phi}^{new} \approx -\mathbf{\Phi}-\frac{\partial\mathbf{\Phi}}{\partial\mathbf{x}}(\mathbf{x}^{new}-\mathbf{x}) =-\mathbf{\Phi}-\mathbf{J}(\mathbf{x}^{new}-\mathbf{x}) \approx -\mathbf{\Phi}-\Delta t\mathbf{J}\mathbf{v}^{new}$

合写成矩阵形式得到 $\begin{bmatrix} \mathbf{M} & -\Delta t \mathbf{J}^T \\ \Delta t \mathbf{J} & \mathbf{C} \end{bmatrix} \begin{bmatrix} \mathbf{v}^{new} \\ \mathbf{\lambda}^{new}\end{bmatrix} = \begin{bmatrix} \mathbf{Mv} \\ -\Phi\end{bmatrix}$

以上推导过程其实没有引入新的关系，只是更换了方程的写法。

称 $\mathbf{x}$ 为主变量，$\mathbf{\lambda}$ 为 $\mathbf{x}$ 的对偶变量。

写成这样的形式，好处在于如果把 $\mathbf{v}^{new}$ 消去先求 $\mathbf{\lambda}^{new}$ ，得到

$(\Delta t^2\mathbf{J}\mathbf{M}\mathbf{J}^T +\mathbf{C}) \mathbf{\lambda}^{new} = -\mathbf{\Phi}-\Delta t\mathbf{J}\mathbf{v}$

劲度 k 越大， $\mathbf{C}=diag(\frac{1}{k},\frac{1}{k},...,\frac{1}{k})$ 越小，反而更容易求解。模拟劲度无穷大的弹簧只需要让 $\mathbf{C}=0$

也可以不消元直接解线性系统 $\begin{bmatrix} \mathbf{M} & -\Delta t \mathbf{J}^T \\ \Delta t \mathbf{J} & \mathbf{C} \end{bmatrix} \begin{bmatrix} \mathbf{v}^{new} \\ \mathbf{\lambda}^{new}\end{bmatrix} = \begin{bmatrix} \mathbf{Mv} \\ -\Phi\end{bmatrix}$

具体处理时两种方法都要注意考虑左边的矩阵是否好求、是否稀疏。

游戏中角色死亡时常用的 Ragdoll Animation（布娃娃动画）可以利用 Constrained Dynamics 方法来实现。

总结

本讲介绍了三种基于约束的方法 PBD, PD 和 Constrained Dynamics，它们都从让弹簧断点满足约束的角度出发。

PBD 直接做投影操作让端点满足约束，不存在能量和力这样的物理量。存在多个弹簧时 PBD 需要多次迭代让多个弹簧都接近满足约束条件的状态。弹簧数越少、迭代次数越多，弹簧的劲度就显得越大。

Strain Limiting 方法先做完一般的物理模拟后再做 PBD 的模拟操作，相当于分成两段处理了物体形变在不同区间的情况，这个思路对任何存在形变的物体都通用，所以 Strain Limiting 被广泛用于基于物理的模拟中。

PD 从投影操作定出了能量，得到的能量和力都与隐式积分法相同，但 Hessian 矩阵不同，可以看作隐式积分的简化版。

Constrained Dynamics 在隐式积分中引入了对偶变量便于模拟劲度 k 较大的情况。

相关论文

Muller. 2008. Hierarchical Position Based Dynamics. VRIPHYS.

Bouaziz et al. 2014. Projective Dynamics: Fusing Constraint Projections for Fast Simulation. TOG (SIGGRAPH).

Tournier et al. 2015. Stable Constrained Dynamics. TOG (SIGGRAPH).

上一篇：GAMES103笔记 Lecture5 基于物理的布料模拟（Physics-based Cloth Simulation）

下一篇：GAMES103笔记 Lecture 7、8 有限元方法（Finite Element Method）

GAMES103 系列笔记目录