GAMES103笔记 Lecture3 刚体动力学（Rigid Body Dynamics）

刚体的平移操作（线性动力学）

物理基础

刚体平移运动的物理原理我们在高中就学过了，核心是下面两条。

位移对时间的导数是速度，速度对时间的导数是加速度： $\dot{x}=v$ , $\ddot{x}=\dot{v}=a$ 。反之，加速度对时间积分等于速度的变化量，速度对时间积分等于位移的变化量： $\Delta \mathbf{v}= \int \mathbf{a}(t) dt$ , $\Delta \mathbf{x}= \int \mathbf{v}(t) dt$

物体在力的作用下产生加速度（牛顿第二定律）： $F=ma$

有了物理定律，就可以在计算机中进行模拟了。

在已知力的情况下，可以直接算出加速度，然后用积分的方式由加速度得到速度和位置。

在编程实践中只能离散化地计算积分。在每一个小时间步，我们认为速度是不变的，有以下几种积分方法。

显式欧拉法

对于时间步 $t=0$ 至 $t=1$，用 $t=0$ 时的速度乘以 $\Delta t$ 来估计该时间步的位移。

对 $t=0$ 泰勒展开可发现二阶以上的项都被抛弃了，因此称显式欧拉法是一阶准确的。

隐式欧拉法

对于时间步 $t=0$ 至 $t=1$，用 $t=1$ 时的速度乘以 $\Delta t$ 来估计该时间步的位移。

隐式欧拉法也是一阶准确的。

显示欧拉法和隐式欧拉法的都因为误差都比较大而不常用。

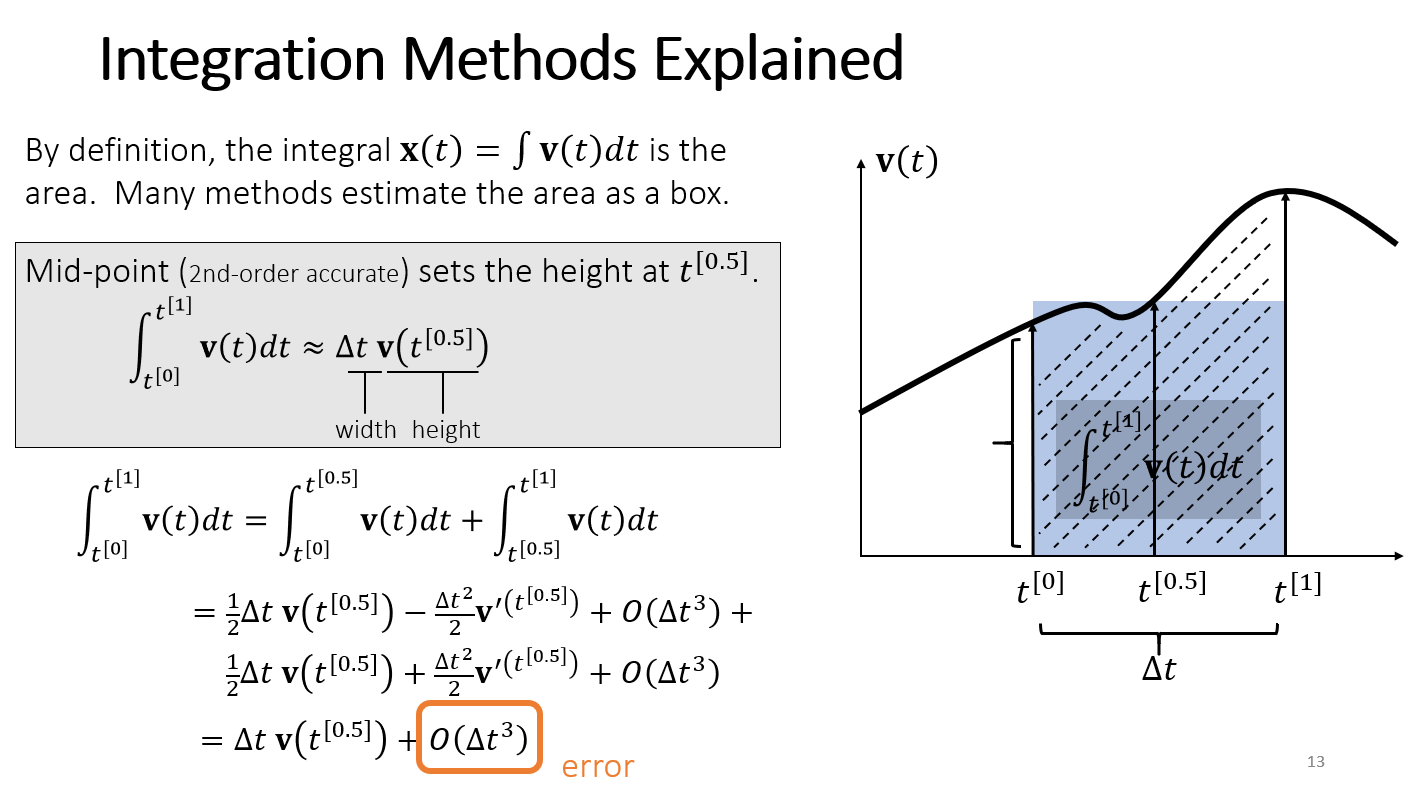
中点法

中点法用 $t=0.5$ 时的速度乘以 $\Delta t$ 来估计该时间步的位移。

分成两段分别对 $t=0.5$ 泰勒展开可发现一阶项相互抵消了，因此中点法是二阶准确的方法。

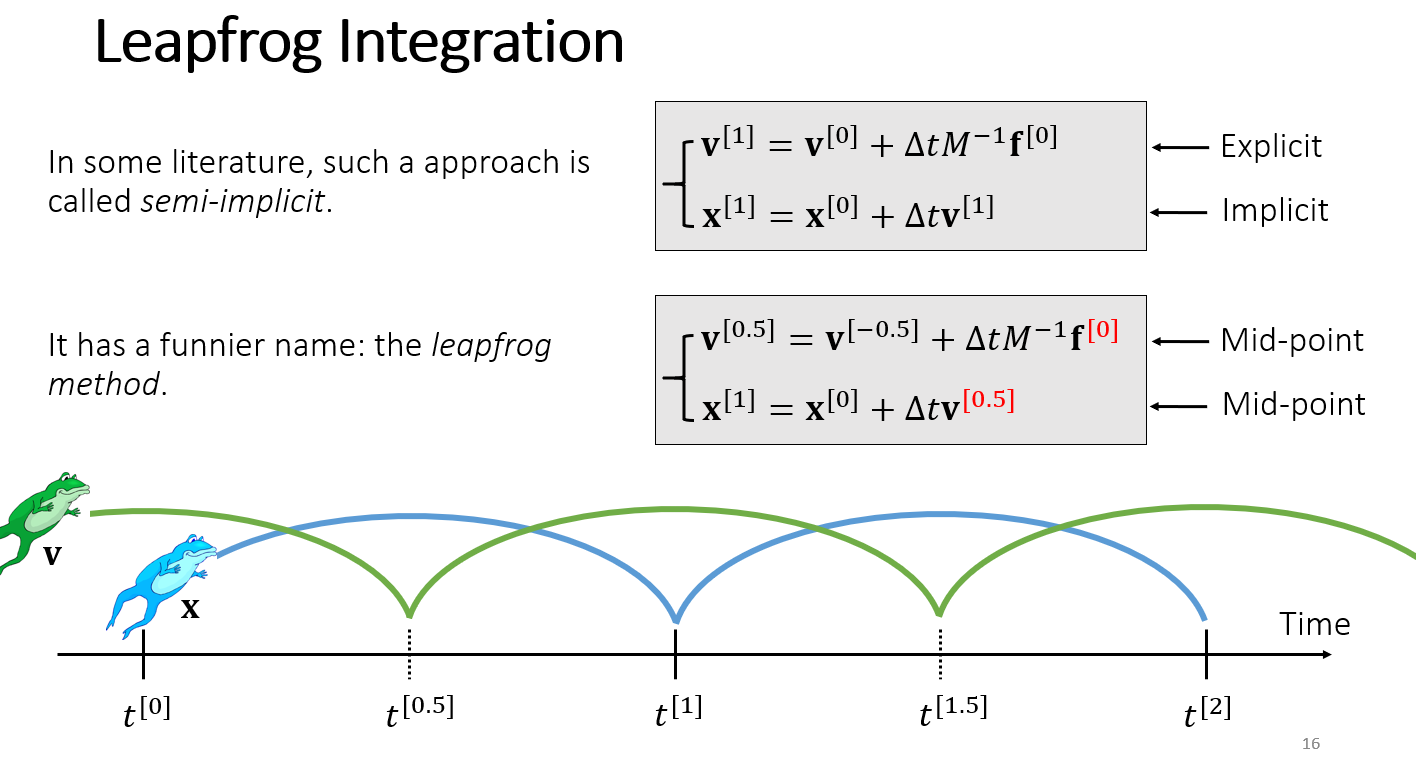
leapfrog方法（半隐式方法）

在游戏中我们先计算出加速度，然后不仅要对速度进行更新，还要对位置进行更新。一般先更新速度，再更新位置。

对于时间步 $t=0$ 至 $t=1$ ，用 $t=0$ 的加速度来计算该时间步的速度变化（显式法），再用刚刚算出的 $t=1$ 的速度来计算该时间步的位移（隐式法）。

如果把速度和位移错开半个时间步，两次更新都是中点法，误差更小。

延伸阅读

根据《游戏引擎架构》，游戏中最常用的数值积分方法是韦尔莱积分法（Verlet integration），另外还有速度韦尔莱积分法（velocity Verlet integration），这两种方法可达到更高的准确度。

刚体的旋转操作（转动动力学）

旋转的表示

在研究如何模拟物理规律之前，我们先考虑一下如何表示一个旋转操作。

旋转矩阵

矩阵天然就表示一个线性变换。

表示纯旋转的矩阵是一个正交矩阵，满足 $R^T=R^{-1}$ 。

如果学过线性代数仍不理解矩阵怎么表示旋转，建议参考3Blue1Brown的《线性代数的本质》系列视频，这个系列视频对线性代数的很多概念做了非常直观的可视化。

用矩阵表示旋转的缺点：

1. 信息存在冗余，旋转实际上只有3个DoFs（自由度），而旋转矩阵用了9个数；
2. 不直观，看到旋转矩阵很难直接想到是怎么旋转的。

欧拉角（Euler Angles）

欧拉角用绕三个固定旋转轴（一般为xyz轴）的三个旋转角度Pitch, Yaw, Roll来表示物体旋转的状态，相比于旋转矩阵更直观一些。

缺点：存在gimbal lock的问题，在某些角度下会丢失自由度。

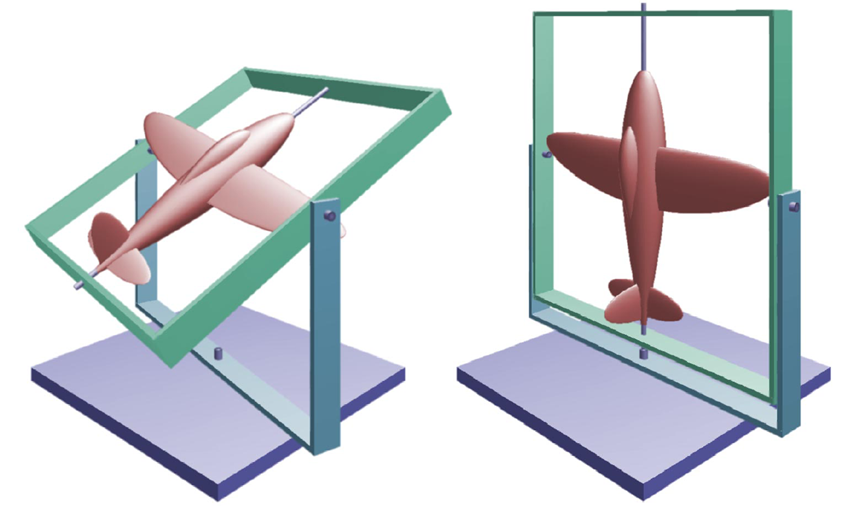
在上图右边的状态下，直接转动飞机和转动蓝色框的效果是一样的，此时只有两个自由度。

四元数（Quaternion）

四元数是一个四维的复数，其实部有一个数，虚部有三个数。

用四元数表示三维空间的旋转不存在gimbal lock的问题，且运算简单快速，由于其良好的性质在游戏中应用非常广泛。

快速了解四元数可阅读 https://www.zhihu.com/question/23005815/answer/33971127

四元数的运算法则

绕旋转轴 $\mathbf{u}$ 转动 $\theta$ 角度的四元数为

$q=[cos(\frac{1}{2}\theta),sin(\frac{1}{2}\theta)\mathbf{u}]$

$q^{-1}=[cos(\frac{1}{2}\theta),-sin(\frac{1}{2}\theta)\mathbf{u}]$

四元数 $q=[w,x,y,z]$ 转换成旋转矩阵

$\mathbf{R}(\boldsymbol{u},\theta)=\left[\begin{array}{ccc}w^{2}+x^{2}-y^{2}-z^{2} & 2(x y-w z) & 2(x z+w y) \\ 2(x y+w z) & w^{2}-x^{2}+y^{2}-z^{2} & 2(y z-w x) \\ 2(x z-w y) & 2(y z+w x) & w^{2}-x^{2}-y^{2}+z^{2}\end{array}\right]$

欧拉角、四元数、旋转矩阵三种表示方法在Unity中的相互转换

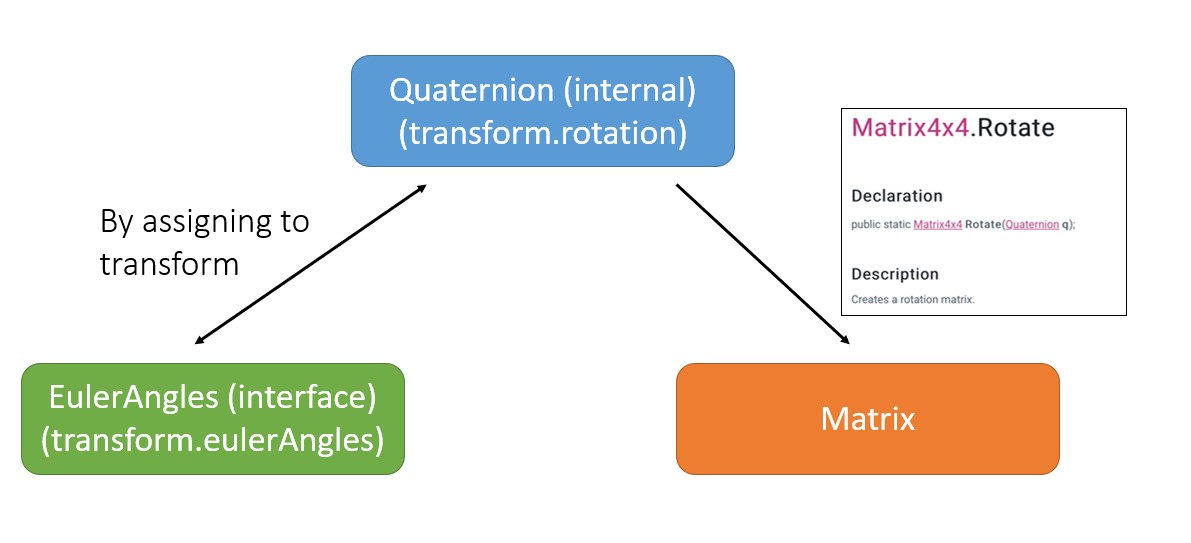
Unity中的transform同时拥有eulerAngles和rotation（四元数）属性，给其中一个赋值，另一个就会自动改变。而Matrix4x4.Rotate函数可以将四元数转换成矩阵。

旋转的物理基础

笔者没学过大学物理，下面几个概念参考了wikipedia

Angular displacement 角移（旋转角度） $\theta$ ，单位为弧度。

Angular velocity 角速度 $\omega=\dot\theta$ ，角速度指向旋转轴的方形，满足右手定则，逆时针旋转时角速度为正。角速度叉乘径向量等于线速度， $v=\omega \times r_i$ 。

Angular acceleration 角加速度 $\alpha=\dot{\omega}=\ddot\theta$ ，角加速度指向旋转轴的方形，满足右手定则，逆时针旋转时角加速度为正。

Torque 力矩 $\tau$ ，使物体产生旋转的趋势，对应于线性动力学中的力。力矩指向旋转轴的方向，满足右手定则，逆时针旋转时力矩为正。

角速度、角加速度、力矩是伪向量（pseudovector）。

Inertia 转动惯量 $I$ ，使物体拥有对抗运动的趋势，对应于线性动力学中的质量。不同方向的转动惯量是不一样的，在三维空间中需要用3x3矩阵来描述一个物体的转动惯量。

类似于 $F=ma$ ，有 $\tau = I\alpha$

力矩的计算

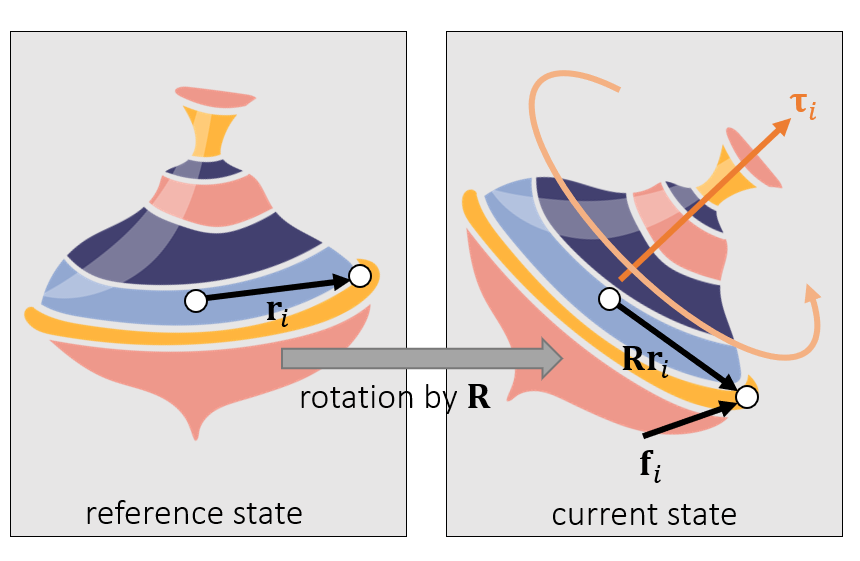
力矩等于径向量与作用力的外积。

$\tau_i=(Rr_i) \times f_i$

物体受到的总力矩是每个力施加力矩的和。

转动惯量的计算

计算转动惯量需要将物体看成一个个小点。

静止状态下 $\mathbf{I}_{\mathbf{r e f}}=\sum m_{i}\left(\mathbf{r}_{i}^{\mathrm{T}} \mathbf{r}_{i} \mathbf{1}-\mathbf{r}_{i} \boldsymbol{r}_{i}^{\mathrm{T}}\right)$ ，其中 $m_i$ 是物体上某一点的质量， $r_i$ 是原点到该点的向量， $\mathbf{1}$ 是单位矩阵。

如果物体旋转了，需要用旋转矩阵 $R$ 乘以每个 $r_i$ ，整理后得到 $\mathbf{I}=\mathbf{R}\mathbf{I}_{\mathbf{ref}}\mathbf{R}^T$

旋转的数值计算，和平移的对比

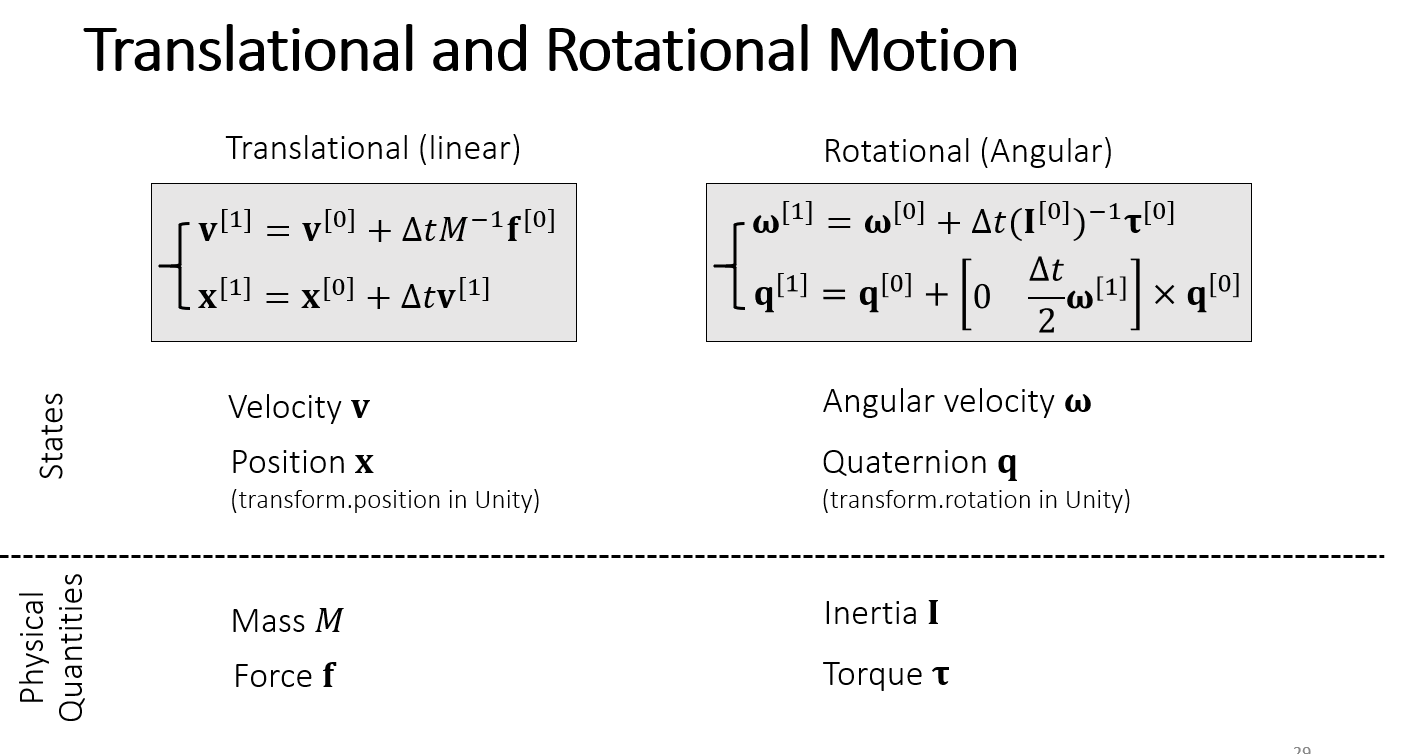
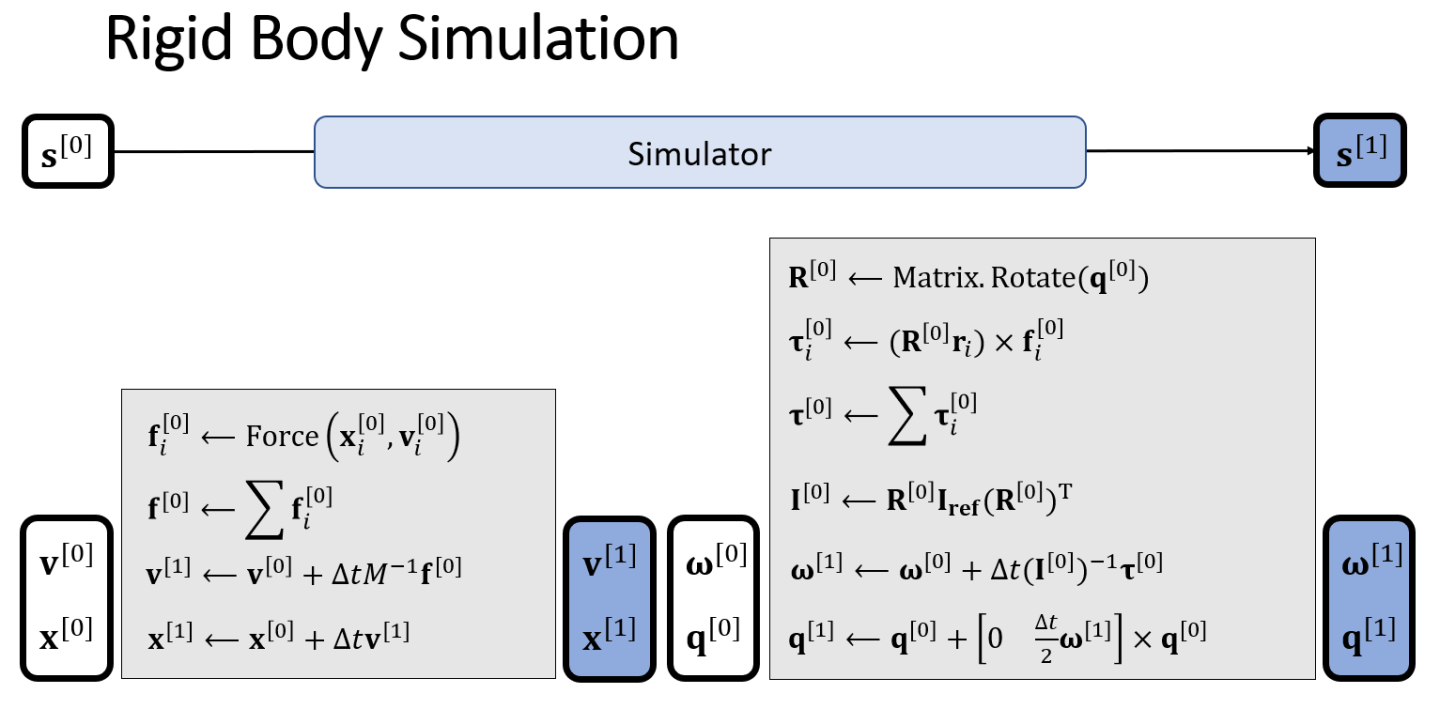
计算旋转的过程如流程图右边部分所示，先由物体当前旋转状态的四元数表示 $q$ 得到旋转矩阵 $R$ ，然后计算每个力产生的力矩并求和，同时根据旋转矩阵计算当前的转动惯量 $I$ ，最后计算 $I^{-1}\tau$ 得到角加速度，更新物体下一时刻的角速度和旋转 $q$ 。

总结

本篇介绍了单个刚体在力的作用下其运动情况如何改变。刚体有平移和旋转两种运动。平移运动的物理基础我们都很熟悉，主要要解决在离散地时间步中求积分的问题。旋转运动需要一些数学基础来对旋转进行表示，还需要用到一些大学物理中的概念。得到力矩和转动惯量后即可采用和平移运动相同的方式来计算积分更新刚体的角速度和旋转状态。

下一篇开始介绍刚体碰撞时如何更新刚体的运动。

上一篇：GAMES103笔记 Lecture2 数学基础

下一篇：GAMES103笔记 Lecture4 刚体碰撞（Rigid Body Contacts）

GAMES103 系列笔记目录