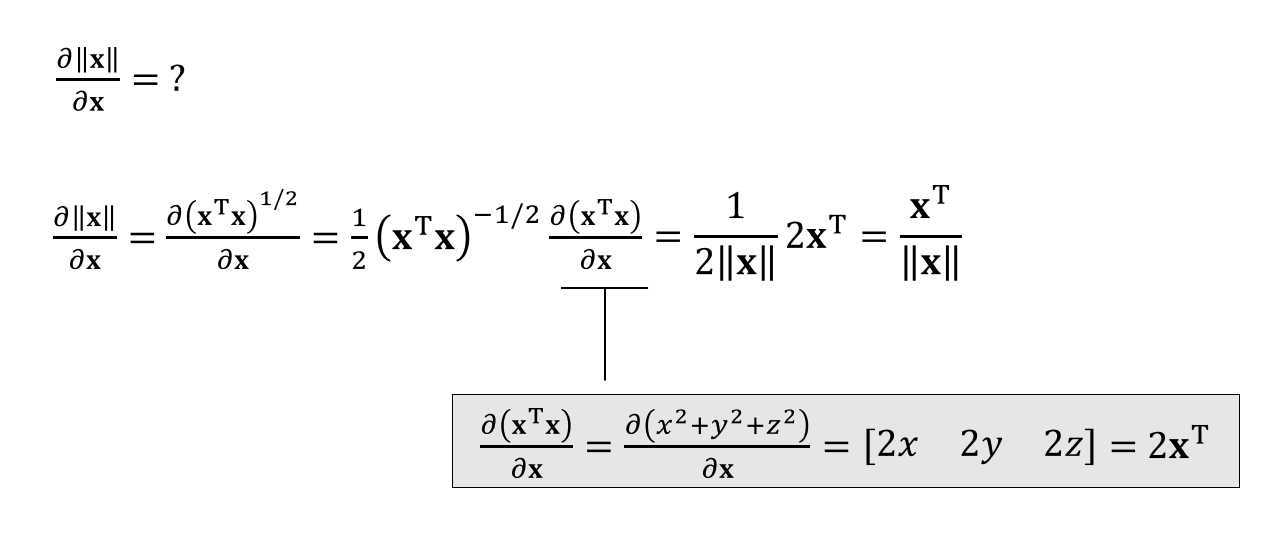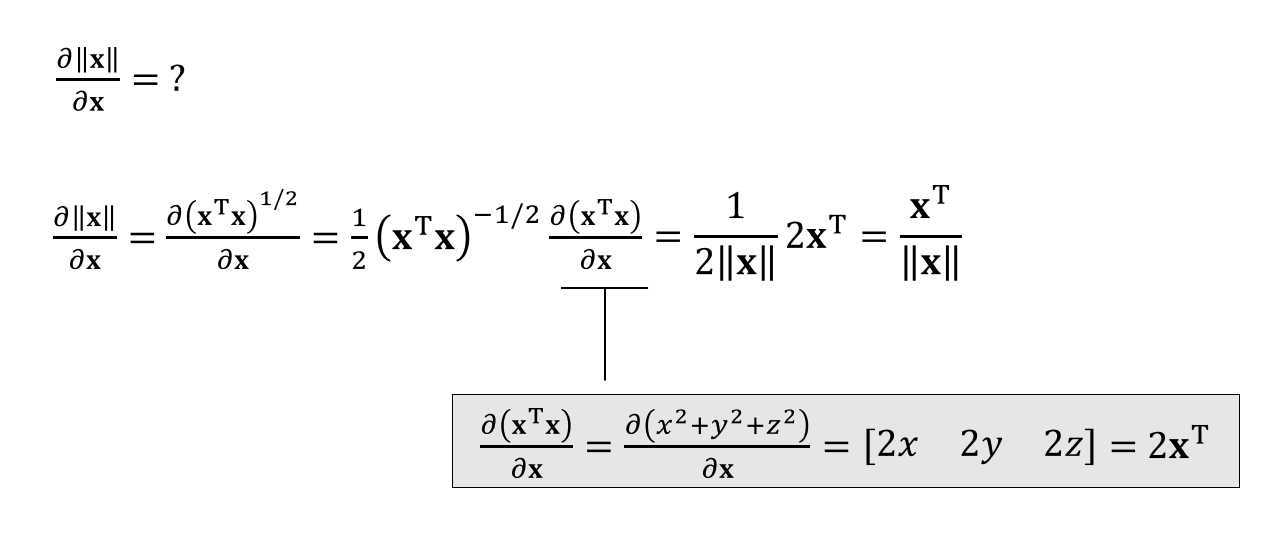抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

GAMES103 Lecture2 数学基础

计算机图形学

发布于：2021年12月1日

次浏览

GAMES103课程主页：GAMES103：基于物理的计算机动画入门 - 计算机图形学与混合现实研讨会

上一篇：GAMES103笔记 Lecture1 基于物理的动画基本介绍

下一篇：GAMES103笔记 Lecture3 刚体动力学（Rigid Body Dynamics）

GAMES103 系列笔记目录

先明确表记方法。

加粗表示一个向量。如 x\mathbf{x} 为一个向量， xx 是一个标量。

向量默认为列向量，即nx1矩阵，是竖着写的，或者横着写加一个转置符号，如 x=[xyz]=[x,y,z]T\mathbf{x} = \begin{bmatrix} x \\ y \\ z\end{bmatrix} = \begin{bmatrix}x,y,z\end{bmatrix}^T

如果是横着写的，会指明为“行向量”。

计算几何

四面体体积

img

四面体重心坐标

img

和三角形重心坐标类似，顶点坐标前的系数为对着的子四面体的体积除以四面体总体积。

线性代数

正定矩阵（s.p.d., symmetric positive definiteness）

实对称矩阵 𝐀 是正定矩阵当且仅当 𝐯T𝐀𝐯>0𝐯^T 𝐀𝐯 > 0 对任意 𝐯≠0𝐯≠0 都成立.

实对称矩阵 𝐀 是半正定矩阵当且仅当 𝐯T𝐀𝐯≥0𝐯^T 𝐀𝐯\geq 0 对任意 𝐯≠0𝐯≠0 都成立.

如果A是正定矩阵，则B=[A−A−AA]B=\begin{bmatrix} A & -A \\ -A & A \end{bmatrix} 一定是半正定矩阵。

证明：

记 x,y\mathbf{x},\mathbf{y} 为两个向量，[xTyT]和[xy]\begin{bmatrix} \mathbf{x}^T & \mathbf{y}^T \end{bmatrix}和\begin{bmatrix} \mathbf{x}\\ \mathbf{y} \end{bmatrix} 是拼接得到的更长的行向量和列向量。

[xTyT]B[xy]=[xTyT][A−A−AA][xy]=(x−y)TA(x−y)⩾0\begin{bmatrix} x^T & y^T \end{bmatrix} B \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} x^T & y^T \end{bmatrix} \begin{bmatrix} A & -A \\ -A & A \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = (\boldsymbol{x}-\boldsymbol{y})^TA(\boldsymbol{x}-\boldsymbol{y})\geqslant0

当且仅当 x=y\boldsymbol{x}=\boldsymbol{y} 时结果等于0，所以B一定是半正定矩阵。

正定矩阵的充分条件

如果一个矩阵满足， aii>Σi≠j∣aij∣a_{ii} > \Sigma_{i \neq j}|a_{ij}| for all i（即每一行中，除掉位于对角线上的那个元素的所有元素之和都小于对角线上的那个元素），则称该矩阵是对角占优的，它必定为正定矩阵。

用这个方法可快速判断矩阵是否正定。

矩阵微积分

多元函数：函数的自变量是一个向量，如 f(x)=f(x,y,z)=x2+y2+z2f(\mathbf{x}) = f(x,y,z)=x^2+y^2+z^2

标量函数：函数的输出是一个标量，如 f(x)=f(x,y,z)=x2+y2+z2f(\mathbf{x}) = f(x,y,z)=x^2+y^2+z^2

向量函数：函数的输出是一个向量，如 f(x)=f(x,y,z)=[P(x,y,z)Q(x,y,z)R(x,y,z)]=[2x,2y,2z]T∈R3\mathbf{f}(\mathbf{x}) = \mathbf{f}(x,y,z)=\begin{bmatrix} P(x,y,z)\\ Q(x,y,z)\\ R(x,y,z) \end{bmatrix} = \begin{bmatrix} 2x, 2y, 2z \end{bmatrix}^T \in R^3

标量函数对向量求导

对向量求导的结果横着写

标量函数对向量求导的结果是行向量

令 x=[x,y,z]T\mathbf{x}= \begin{bmatrix} x, y, z \end{bmatrix}^T , f(x)∈Rf(\mathbf{x}) \in R ，则：

df=∂f∂xdx+∂f∂ydy+∂f∂zdz=[∂f∂x,∂f∂y,∂f∂z][dxdydz]df=\frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy + \frac{\partial f}{\partial z}dz = \begin{bmatrix} \frac{\partial f}{\partial x} , \frac{\partial f}{\partial y} , \frac{\partial f}{\partial z} \end{bmatrix} \begin{bmatrix} dx \\ dy \\ dz \end{bmatrix}

dx=[dxdydz]d\mathbf{x} = \begin{bmatrix} dx \\ dy \\ dz\end{bmatrix}

∂f∂x=[∂f∂x,∂f∂y,∂f∂z]\frac{\partial f}{\partial \mathbf{x}} = \begin{bmatrix} \frac{\partial f}{\partial x} , \frac{\partial f}{\partial y} , \frac{\partial f}{\partial z} \end{bmatrix}

标量函数的梯度

标量函数的梯度是一个向量，等于对向量求导的转置

对于多元函数 f(x)f(\mathbf{x})

∇f=[∂f∂x∂f∂y∂f∂z]=[∂f∂x,∂f∂y,∂f∂z]T=[∂f∂x]T\nabla f = \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \\ \frac{\partial f}{\partial z} \end{bmatrix} = \begin{bmatrix} \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} , \frac{\partial f}{\partial z} \end{bmatrix}^T = [\frac{\partial f}{\partial \mathbf{x}} ]^T

可以把梯度算子 ∇\nabla 看作向量 [∂∂x,∂∂y,∂∂z]T\begin{bmatrix} \frac{\partial }{\partial x} , \frac{\partial }{\partial y}, \frac{\partial }{\partial z} \end{bmatrix}^T

Jacobian Matrix、散度、旋度

向量函数对自变量求导，得到一个矩阵，称为 Jacobian Matrix（雅可比矩阵）

对于向量函数 f(x)=[P(x)Q(x)R(x)]∈R3\boldsymbol{f}(\mathbf{x}) = \begin{bmatrix} P(\mathbf{x})\\ Q(\mathbf{x})\\ R(\mathbf{x}) \end{bmatrix} \in R^3

J(x)=∂f∂x=[∂P∂x∂P∂y∂P∂z∂Q∂x∂Q∂y∂Q∂z∂R∂x∂R∂y∂R∂z]J(\mathbf{x})=\frac{\partial\mathbf{f}}{\partial\mathbf{x}}=\begin{bmatrix} \frac{\partial P}{\partial x} & \frac{\partial P}{\partial y} & \frac{\partial P}{\partial z} \\ \frac{\partial Q}{\partial x} & \frac{\partial Q}{\partial y} & \frac{\partial Q}{\partial z} \\ \frac{\partial R}{\partial x} & \frac{\partial R}{\partial y} & \frac{\partial R}{\partial z} \end{bmatrix} （上边向量 f\mathbf{f} 求导后仍然竖着写，下边对向量 x\mathbf{x} 求导横着写）

散度（divergence）

向量函数的散度等于其雅可比矩阵的迹，是一个标量

div f=∇⋅f=∂P∂x+∂Q∂y+∂R∂zdiv\ \mathbf{f} = \nabla \cdot \boldsymbol{f} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}

旋度（curl, rotation）

向量函数的旋度还是一个向量

∇×f=∣ijk∂∂x∂∂y∂∂zPQR∣=[∂R∂y−∂Q∂z∂P∂z−∂R∂x∂Q∂x−∂P∂y]\nabla \times \boldsymbol{f} = \left|\begin{array}{c} i & j & k \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \end{array}\right| = \begin{bmatrix} \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \\ \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \\ \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \end{bmatrix}

Hessian Matrix（海森矩阵）

对于多元函数 f(x)∈Rf(\mathbf{x}) \in R ，其梯度的雅可比矩阵称作海森矩阵

H=∂∇f∂(x)=[∂2f∂x2∂2f∂x∂y∂2f∂x∂z∂2f∂x∂y∂2f∂y2∂2f∂y∂z∂2f∂x∂z∂2f∂y∂z∂2f∂z2]H = \frac{\partial \nabla \mathbf{f}}{\partial(\mathbf{x})} = \begin{bmatrix} \frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial x \partial z} \\ \frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial y^2} & \frac{\partial^2 f}{\partial y \partial z}\\ \frac{\partial^2 f}{\partial x \partial z} & \frac{\partial^2 f}{\partial y \partial z} & \frac{\partial^2 f}{\partial z^2} \end{bmatrix}

当两个二阶偏导函数（如 ∂2f∂x∂y\frac{\partial^2 f}{\partial x \partial y} 和 ∂2f∂y∂x\frac{\partial^2 f}{\partial y \partial x} ）在某一点都连续时，函数在该点可微，求导顺序不影响在这一点的求导结果，所以这里把 Hessian 矩阵写作对称矩阵。

如果 Hessian 矩阵是正定矩阵，则函数在该点为凸函数。如果梯度为0，则该点为函数的极小值。

如果一个函数的 Hessian 在定义域上一直是正定矩阵，则该函数只存在一个极小值，也是函数的最小值。

Laplacian算子

Δf=∇⋅∇f=∇2f=∂2f∂x2+∂2f∂y2+∂2f∂z2\Delta f = \nabla \cdot \nabla f = \nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2}

泰勒公式

f(x)=f(x0)+∂f(x0)∂x(x−x0)+12∂2f(x0)∂x2(x−x0)2+...=f(x0)+[∇f(x0)]T(x−x0)+12![x−x0]TH(x0)[x−x0]+on\begin{aligned} f(\mathbf{x}) &= f\left(\mathbf{x}_{0}\right) + \frac{\partial f(\mathbf{x_0})}{\partial \mathbf{x}}(\mathbf{x} - \mathbf{x_0}) + \frac{1}{2} \frac{\partial^2 f(\mathbf{x_0})}{\partial \mathbf{x}^2}(\mathbf{x} - \mathbf{x_0})^2 + ... \\ &=f\left(\mathbf{x}_{0}\right)+\left[\nabla f\left(\mathbf{x}_{0}\right)\right]^{T}\left(\mathbf{x}-\mathbf{x}_{0}\right)+\frac{1}{2 !}\left[\mathbf{x}-\mathbf{x}_{0}\right]^{T} H\left(\mathbf{x}_{0}\right)\left[\mathbf{x}-\mathbf{x}_{0}\right]+o^{n} \end{aligned}

这里的H是Hessian矩阵， H(x0)=[∂2f(x0)∂x12∂2f(x0)∂x1∂x2⋯∂2f(x0)∂x1∂xn∂2f(x0)∂x2∂x1∂2f(x0)∂x22⋯∂2f(x0)∂x2∂xn⋮⋮⋱⋮∂2f(x0)∂xn∂x1∂2f(x0)∂xn∂x2⋯∂2f(x0)∂xn2]H\left(\mathbf{x}_{0}\right)=\left[\begin{array}{cccc}{\frac{\partial^{2} f\left(x_{0}\right)}{\partial x_{1}^{2}}} & {\frac{\partial^{2} f\left(x_{0}\right)}{\partial x_{1} \partial x_{2}}} & {\cdots} & {\frac{\partial^{2} f\left(x_{0}\right)}{\partial x_{1} \partial x_{n}}} \\ {\frac{\partial^{2} f\left(x_{0}\right)}{\partial x_{2} \partial x_{1}}} & {\frac{\partial^{2} f\left(x_{0}\right)}{\partial x_{2}^{2}}} & {\cdots} & {\frac{\partial^{2} f\left(x_{0}\right)}{\partial x_{2} \partial x_{n}}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\frac{\partial^{2} f\left(x_{0}\right)}{\partial x_{n} \partial x_{1}}} & {\frac{\partial^{2} f\left(x_{0}\right)}{\partial x_{n} \partial x_{2}}} & {\cdots} & {\frac{\partial^{2} f\left(x_{0}\right)}{\partial x_{n}^{2}}}\end{array}\right]

如果H是正定矩阵，则二阶项大于0。

向量的长度对自身求导

Reference

  1. GAMES103
  2. https://atmos.uw.edu/~dennis/MatrixCalculus.pdf

笔者之前只学过工科的微积分、线代、概率论，笔记中可能存在错误和解释不清的地方，欢迎大佬以及和我一样的萌新来多多交流讨论，对于错误的部分希望能毫不留情的指正。

如果文章对你有帮助的话，就去知乎点个赞鼓励一下我吧~ 特别是点收藏的朋友们麻烦收藏前先点个赞同，谢谢啦 ♪(･ω･)ﾉ

上一篇：GAMES103笔记 Lecture1 基于物理的动画基本介绍

下一篇：GAMES103笔记 Lecture3 刚体动力学（Rigid Body Dynamics）

GAMES103 系列笔记目录

GAMES103

物理模拟

评论